YGS-LYS Mutlak Değer
Konu Anlatımı
Soru Çözümleri
Testler
...
Matematikte mutlak değer (ya da mutlak değer fonksiyonu bir gerçel sayının işaretsiz sayısal değerini verir. Örneğin
mutlak değer (ya da mutlak değer fonksiyonu bir gerçel sayının işaretsiz sayısal değerini verir. Örneğin 3; hem 3'ün hem de −3'ün mutlak değeridir. Bilgisayarlarda ise
3; hem 3'ün hem de −3'ün mutlak değeridir. Bilgisayarlarda ise bu fonksiyonu ifade etmek için kullanılan matematiksel fonksiyon genelde abs(...)'dir (Örneğin: abs(−8)=|−8|=8 gibi).
bu fonksiyonu ifade etmek için kullanılan matematiksel fonksiyon genelde abs(...)'dir (Örneğin: abs(−8)=|−8|=8 gibi).
Mutlak değer fonksiyonunun gerçel sayılarla kullanımı dışında geniş bir matematiksel kullanım alanı vardır. Örneğin
geniş bir matematiksel kullanım alanı vardır. Örneğin mutlak değer karmaşık sayılar gibi kümeler için de tanımlanabilir.
mutlak değer karmaşık sayılar gibi kümeler için de tanımlanabilir.
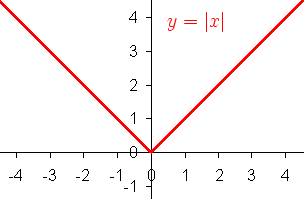 Mutlak değer fonksiyonunun gerçel sayılardaki grafiği.
Mutlak değer fonksiyonunun gerçel sayılardaki grafiği.
[değiştir]
Gerçel sayılar
Her a gerçel sayısının mutlak değeri | a |
gerçel sayısının mutlak değeri | a |  şeklinde ifade edilir ve şu şekilde tanımlanır:
şeklinde ifade edilir ve şu şekilde tanımlanır:
 Yukarıda da görüldüğü gibi a'nın mutlak değeri ya artı ya da sıfır değerini alacak
Yukarıda da görüldüğü gibi a'nın mutlak değeri ya artı ya da sıfır değerini alacak hiç bir zaman eksi değeri almayacaktır.
hiç bir zaman eksi değeri almayacaktır.
Geometrik anlamda bir gerçel sayının mutlak değeri onun sayı doğrusunda sıfıra olan uzaklığıdır. Daha genel anlamdaysa mutlak değer iki reel sayı arasındaki farkı
bir gerçel sayının mutlak değeri onun sayı doğrusunda sıfıra olan uzaklığıdır. Daha genel anlamdaysa mutlak değer iki reel sayı arasındaki farkı sayı doğrusunda aralarındaki uzaklık olarak verir.
sayı doğrusunda aralarındaki uzaklık olarak verir.
Aşağıdaki yordamlar bir mutlak değerin çözümünde yardımcı olabilecek önermeler içerir.
1. ÖNERME:
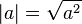
2. ÖNERME:
Mutlak değer aşağıdaki dört temel özelliğe sahiptir:
 Negatif olmama
Negatif olmama 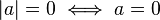 Sıfır eşitliği
Sıfır eşitliği  Çarpanlara ayrılabilme
Çarpanlara ayrılabilme  Alt toplananlara ayrılabilme
Alt toplananlara ayrılabilme
3. ÖNERME:
Mutlak değerin diğer önemli özellikleri ise:
 Simetri
Simetri 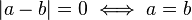 a ve b eştir
a ve b eştir 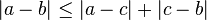 Üçgen eşitsizliği
Üçgen eşitsizliği  Bölmenin ayrılması (çarpanlara ayrılabilirlik gibi)
Bölmenin ayrılması (çarpanlara ayrılabilirlik gibi)  (Alt toplananlara ayrılabilirlik)
(Alt toplananlara ayrılabilirlik)
Diğer iki kullanışlı eşitsizlikler ise:

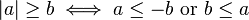
Aşağıdakilerse genelde eşitsizlik çözümünde kullanılır; örneğin:


 [değiştir]
[değiştir]
Karmaşık sayılar

Karmaşık sayılara kadar olan kısımda verilen mutlak değer özellikleri karmaşık sayılar kümesine aynen uygulanamaz. Önerme 1'i ele alırsak:
verilen mutlak değer özellikleri karmaşık sayılar kümesine aynen uygulanamaz. Önerme 1'i ele alırsak:
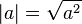 her gerçel sayının bir karmaşık sayı olduğunu ve
her gerçel sayının bir karmaşık sayı olduğunu ve
bir karmaşık sayının
 olduğunu düşünürsek göreceğiz ki
olduğunu düşünürsek göreceğiz ki gerçel sayılarda y katsayısı 0'a eşit. Öyleyse gerçekte z'nin mutlak değer (ya da karmaşık sayılarda bazen modül olarak adlandırılır) şu şekilde tanımlanabilir.
gerçel sayılarda y katsayısı 0'a eşit. Öyleyse gerçekte z'nin mutlak değer (ya da karmaşık sayılarda bazen modül olarak adlandırılır) şu şekilde tanımlanabilir.
 Öyleyse bir gerçel sayıda bu işlemi şöyle gerçekleştirebiliriz:
Öyleyse bir gerçel sayıda bu işlemi şöyle gerçekleştirebiliriz:
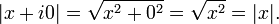 Mutlak değer bir sayının orijine uzaklığını verir. Karmaşık sayılar iki boyutlu düzlem üzerinde incelendiğinden Pisagor teoremi iki nokta arasındaki uzaklığı bulmada işimize yarayacaktır.Karmaşık düzlemde iki karmaşık sayı arasındaki uzunluğu bulmak içinse aynı gerçel sayılardaki gibi iki sayının farkının mutlak değerini alırız.
Mutlak değer bir sayının orijine uzaklığını verir. Karmaşık sayılar iki boyutlu düzlem üzerinde incelendiğinden Pisagor teoremi iki nokta arasındaki uzaklığı bulmada işimize yarayacaktır.Karmaşık düzlemde iki karmaşık sayı arasındaki uzunluğu bulmak içinse aynı gerçel sayılardaki gibi iki sayının farkının mutlak değerini alırız.
Karmaşık sayılar yukarıda verilen 2. ve 3. önermelerin tüm özelliklerini taşır. Bununla beraber
 ise
ise ve
ve
 z karmaşık sayısının eşlenik'i ise
z karmaşık sayısının eşlenik'i ise açıkça görülür ki:
açıkça görülür ki:

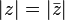
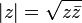
doğru üzerinde x sayısının sıfıra olan uzaklığına x in mutlak değeri denir ve │x│ ile gösterilir.
x R nin elemanıdır ve
R nin elemanıdır ve
│x│ ={x x > 0 ise
x > 0 ise
{-x x < 0 ise
x < 0 ise
şeklinde tanımlanır.
│f(x)│ ={f(x) f(x) > 0 ise
f(x) > 0 ise
{-f(x) f(x)< 0 ise
f(x)< 0 ise
Örnek: x =-3 için │x-5│ - │x+2│ ifadesinin eşiti kaçtır?
Çözüm: │-3-5│ - │-3+2 │ = 8-1=7
Örnek: a<b<0olduğuna göre
│a+b│ - │a-b │ ifadesinin eşiti nedir?
Çözüm: │a+b│ - │a-b│ = -(a+b) -[ -(a-b) ]
=-a-b+a-b
=-2b
ÖZELLİKLERİ
a b elemandır R için
b elemandır R için
1) │a│≥ 0 dır
2) │a │ = │ -a│
3) - │ a│≤a ≤│a│
4) │a.b│ = │a│.│b │
5) b�* 0 için │a/b │= │a│ / │b │
6) │IaI-IbI│≤│a+b│ < │a│ + │b │ (üçgen eşitsizliği)
7) n elemanıdır Z+ olmak üzere │an │ = │a│n
8) a> 0 x elemanıdır R ve │x│< a ise -a <x <a
x elemanıdır R ve │x│< a ise -a <x <a
9) a>0 x elemanıdır R
x elemanıdır R │x│≥ a ise x≥ a veya x ≤ -a dır.
│x│≥ a ise x≥ a veya x ≤ -a dır.
10)I-aI=IaI Ia-bI=Ib-aI
Ia-bI=Ib-aI
11)I f(x) I = a ise f(x )= a veya f(x) = -a
12)I f(x) I < a ise -a< f(x) < a
13)I f(x) I > a ise f(x) > a U -f(x) > a
İSPATLAR
Öz.1)a = 0 ise IaI = I0I = 0
a > 0 ise IaI = a >0
a < 0 ise IaI = -a >0 dır.
O halde IaI > 0 dır.
Öz.2)a ve -a sayılarının 0 dan uzaklıkları eşit olduğundan IaI=I-aI dır.
Öz.6) a elemanıdır R için -IaI ≤ a ≤ IaI
b elemanıdır R için -IbI ≤ b≤ IbI
+
-IaI-IbI≤a+b≤IaI+IbI
O halde Ia+bI < IaI+IbI dir.
Öz.7) a b elemanıdır R için Ia.bI=IaI.IbI idi.
b elemanıdır R için Ia.bI=IaI.IbI idi.
Ia nI=Ia.a.a...aI=IaI.IaI.IaI...IaI=IaIn dir.
(n tane) ( n tane )
Öz.3)a sayısı için a<0 a=0
a=0 a>0 durumlarından biri vardır.
a>0 durumlarından biri vardır.
a)a < 0 ise IaI = -a dır.
IaI > 0 olduğundan -IaI < 0 dır.
-IaI= a <0 < IaI ise -IaI < a < IaI dır.
b)a=0 ise IaI = I0I = 0 ve -Ia I= 0 olacağından –IaI < a < IaI dır.
c)a > 0 ise IaI = a ve -IaI < 0 dır.
-IaI≤ 0≤ IaI = a ise -IaI < a < IaI dır.
MUTLAK DEĞERLİ DENKLEMLER
Soru: I3x-7I = 5 denklemini çözünüz.
Çözüm:I3x-7I = 5 ise; 3x-7 = 5 veya 3x-7 = -5 olur.
1- 3x-7 = 5 2- 3x-7=-5
3x = 12 3x = 2
x = 4 x = 2/3
Ç={4 2/3}
2/3}
Soru:Ix-7I = 7-x eşitliğini sağlayan kaç tane doğal sayı vardır?
Çözüm: Ix-7I = 7-x ise
x-7 < 0 ise x < 7olup x doğal sayıları 0 1
1 2
2 3
3 4
4 5
5 6
6 7 dir.
7 dir.
O halde 8 tane doğal sayı vardır.
Soru: = 2 denkleminin çözüm kümesi nedir ?
Çözüm: = 2
5-2x/3=2 veya 5-2x/3= -2
5-2x = 6 veya 5-2x = -6
x = -1/2 veya x = 11/2
Ç ={-1/2 11/2}
11/2}
Soru:I 4+I2x-3I I = 5 denklemini sağlayan x reel sayılarının toplamı nedir?
Çözüm: I 4+I2x-3I I = 5
4+I2x-3I = 5 veya 4+I2x-3I = -5
I2x-3I = 1 veya I2x-3I = -9
2x-3 = 1 veya 2x-3 = -1 Çözüm:O
x = 2 x = 1
O halde x+x = 2+1 = 3 olur.
Uyarı:Hiçbir reel sayının mutlak değeri negatif olamayacağından denklemin çözüm kümesi boş küme () olur.
denklemin çözüm kümesi boş küme () olur.
MUTLAK DEĞERLİ EŞİTSİZLİKLER
Soru: Ix-7I < 3 eşitsizliğinin çözüm kümesini bulunuz.
Çözüm: Ix-7I < 3 = -3 < x-7 < 3 = -3+7 < x < 3+7
=4<x<10 Ç={5 6
6 7
7 8
8 9}
9}
Soru:I 3x+2 I+9 > 2 eşitsizliğini çözünüz.
Çözüm:I 3x+2I+9 > 2 = I 3x+2I > -7
***Bu eşitsizlik x in her değeri için sağlanır.Bu nedenle; Çözüm kümesi R dir.
Soru: I Ix-5I-2 I < 3 eşitsizliğini sağlayan kaç tane tamsayı vardır?
Çözüm:I Ix-5I-2 I < 3 = -3 < Ix-5I -2 < 3
= -1 < Ix-5I < 5
Ix-5I >-1 eşitsizliği daima doğrudur.
Ix-5I < 5 = -5 < x-5 < 5
= 0 < x < 10
Bu aradaki tamsayılar 1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9 olup 9 tamsayı vardır.
9 olup 9 tamsayı vardır.
Soru: I 2x-7 I < 2 eşitsizliğini sağlayan kaç tane tamsayı vardır?
Çözüm:I 2x-7 I < 2 = -2 < 2x-7 < 2
= -2+7 < 2x < 2+7
= 5 < 2x < 9
= 5/2 < x < 9/2
Bu durumda çözüm kümesi {3 4} olur.
4} olur.
Soru: I 3x+1 I > -8 denkleminin çözüm kümesini bulunuz.
Çözüm: x elemanıdır R için I 3x+1 I > 0 olduğundan
I 3x+1 I > -8 eşitsizliği daima doğrudur. Buna göre denklemin çözüm kümesi Reel sayılar kümesidir.
Soru: I 3-3x I < 9 eşitsizliğinin R deki çözüm kümesi nedir?
a) 0<x<2 b) -2<x<4 c) -1<x<0 d) 0<x<2 e) 2<x<4
Çözüm: I 3-3x I<9 = -9 < 3-3x < 9
= -9+3 < 3x < 9+3
= -6 < 3x < 12
= -6/3 < x < 12/3
= -2 < x < 4 ( Cevap B dir.)
Soru: 1 < Ix-2I < 3 eşitsizliğini sağlayan kaç tane tamsayı vardır?
Çözüm: 1 < Ix-2I < 3 = 1 < x-2 < 3
= 1+2 < x < 3+2
= 3 < x < 5
Eşitsizliği oluşturan tamsayılar = {3 4
4 5} tir.
5} tir.
MUTLAK DEĞER İLE İLGİLİ KARIŞIK
ALIŞTIRMALAR
Soru 3: |x| 2 => -2<x<2 dir.
Soru 4: |x| 2 => x > 2 veya x < -2 dir.
Soru 5: |x-1| = 3 => x-1=3 veya x - 1 = -3
x = 4 veya x = -2 dir.
Soru 6: a<b<0<c olmak üzere;
a +c + b-c+c - a
= -a + c - (b - c) + c – a
= -a + c-b + c + c- a
= 3c - 2a - b dir.
Soru 7:x-5= 3 => x - 5 = 3 veya x -5 = -3 tür.
x = 8 veya x = 2
x = 8 veya x =- 8 veya
x = 2 veya x =- 2 dir.
Ç.K. = {-8 -2
-2 2
2 8} dir.
8} dir.
Soru 8: ||x-l| + 4| = 6=>x-1 + 4 = 6 veya
x-1 + 4 = -6 lx-1l = 2 veya lx-1l = -10 olur.
x-1 = - 10 olamayacağından kök yoktur.
x-1 = 2 ise x - 1 = 2 veya x - 1 = -2 x = 3 veya x = -1 dir.
Ç.K = {-1 3}
3}
Soru 9: I 3x-1 I+5 = 0 denkleminin çözüm kümesi nedir?
Çözüm: I 3x-1 I+5 = 0 ise I 3x-1 I = -5 olur.
*** a elemanıdır R için IaI > 0 dır.
Bu nedenle sorunun çözüm kümesi O dir.
Soru 10: I Ix-4I -5 I = 10 denklemini sağlayan x değerlerini bulunuz.
Çözüm: I Ix-4I –5 I = 10
Ix-4I-5 =10 veya Ix-4I-5 = -10
Ix-4I = 5 veya Ix-4I = -5
Ç = {O}
x-4 = 15 veya x-4 = -15 x = 19 veya x = -14
Soru11: I Ix-1I+5 I = 8 denkleminin kökleri toplamı kaçtır?
a) -2 b) 0 c) 2 d) 4 e)14
Çözüm: I Ix-1I+5 I = 8
I Ix-1I+5 I = 8 veya I Ix-1I+5 = -8
Ix-1I = 3 veya Ix-1I = -13
Ç = {O}
x-1 = 3 veya x-1 = -3
x = 4 veya x = -2
x+x = 4+(-2) = 2 ( Cevap C dir.)
Soru 12: I Ix-2I-3 I = 7 denkleminin kökleri toplamı kaçtır?
a) 2 b) 4 c) 8 d) 10 e) 12
Çözüm: I Ix-2I-3 I = 7
Ix-2I-3 = 7 veya Ix-2I-3 = -7
Ix-2I = 10 veya Ix-2I = -4
Ç = {O}
x-2 = 10 veya x-2 = -10
x = 12 veya x = -8
x+x = 12-(-8) = 4 ( Cevap B dir.)
Soru 13: I 7-(3-I-5I) I işleminin sonucu nedir?
A) 4 B) 5 C) 6 D) 7 E) 9
Çözüm:
I 7-(3-I-5I) I = I 7-[3- -(-5)] I
= I 7-[3-5] I
= I 7-(-2) I
= I 7+2 I
= I 9 I = 9
Soru 14: I Ix-2I-5 I = 1 denklemini sağlayan x tam sayıları nelerdir?
a) 3 6
6 -3
-3 -6 b) 4
-6 b) 4 8
8 -3
-3 -8 c) 7
-8 c) 7 9
9 5 d) 8
5 d) 8 -4
-4 6
6 -2 e) 2
-2 e) 2 -2
-2
Çözüm: I Ix-2I-5 I
Ix-2I-5 = 1 veya Ix-2I-5 = -1
Ix-2I = 6 veya Ix-2I = 4
x-2 = 6 veya x-2 = -6 x-2 = 4 veya x-2 = -4
x = 8 x = -4 x = 6 x = -2
Soru 15: Ix+2I < 4 eşitsizliğini sağlayan kaç tane tamsayı vardır?
a) 13 b) 9 c) 8 d) 7 e) 6 (ÖSS 1999)
Çözüm:
Ix+2I < 4 = -4 < x + 2 <4
= -6 < x < 2
Eşitsizliği oluşturan tamsayılar –6 -5
-5 -4
-4 -3
-3 -2
-2 -1
-1 0
0 1
1 2 dir. ( Cevap A dır.)
2 dir. ( Cevap A dır.)
Soru 16: IxI < 6 olduğuna göre x-2y+2 = 0 koşulunu sağlayan kaç tane y tamsayısı vardır?
x-2y+2 = 0 koşulunu sağlayan kaç tane y tamsayısı vardır?
a) 7 b) 6 c) 5 d) 4 e) 3 (ÖSS 2000)
Çözüm:
IxI 0 dan küçük olmayacağından IxI 0 1
1 2
2 3
3 4
4 5
5 6 olabilir.
6 olabilir.
x-2y+2 = 0 koşulunu çift sayılar oluşturur.Bunlar 0 2
2 4
4 6 dır.Bu sayılar y yi tamsayı yapar. ( Cevap D dir.)
6 dır.Bu sayılar y yi tamsayı yapar. ( Cevap D dir.)
Soru 17:
f(x) = 12 fonksiyonunun en büyük değeri
Ix-1I+Ix+3I
nedir?
a) 2 b) 3 c) 4 d) 5 e) 6
Çözüm:
x elemanıdır [-3 1] için f(x) en büyük olur. X = -3 ise
1] için f(x) en büyük olur. X = -3 ise
f(-3) = 12 = 12/4 =3 tür.
I-3-1I+I-3+3I
( Cevap B dir.)
Soru 18:x-1 6 olduğuna göre x - 2y + 2 = O koşulunu sağlayan kaç tane y tamsayısı vardır?
x - 2y + 2 = O koşulunu sağlayan kaç tane y tamsayısı vardır?
A) 7 B) 6 C) 5 D) 4 E) 3 (2000-ÖSS)
ÇÖZÜM
x-2y + 2 = 0 => x = 2y- 2 dir.
x < 6 => 2y - 2 6 => -6 2y - 2 < 6 dır.
Buradan -4 < 2y < 8 => -2 < y < 4 bulunur.
-4 < 2y < 8 => -2 < y < 4 bulunur.
Bu koşulu sağlayan y tamsayıları -2 -1
-1 0
0 1
1 2
2 3
3 4 olup 7 tanedir.
4 olup 7 tanedir.
Cevap: A'dır.
Soru 19:x+24 eşitsizliğini sağlayan kaç tane tamsayı vardır?
A) 13 B) 9 C) 8 D) 7 E) 6 (1999-ÖSS)
ÇÖZÜM
x+24 ise < 4 ise -4 < x + 2 < 4
-4-2<x+2-2<4-2
-6 < x < 2
x = -6 -5
-5 -4
-4 -3
-3 -2
-2 -1
-1 O
O 1
1 2 olup 9 tane tamsayı değeri vardır.
2 olup 9 tane tamsayı değeri vardır.
Cevap: B'dir.
Soru 20: x < 0 olmak üzere x-|x-8| - 8 ifadesi aşağı�*dakilerden hangisine eşittir?
A)16 B)-2x C)-4x D)-2x+16 E)-4x+16 (1999-ÖSS)
ÇÖZÜM
x-|x-8| - 8 = ?
x-8| = -(x-8) = -x+8
(-)
= x-(-x+8) - 8 |2x-8|-8
(-)
= - (2x - 8) - 8 = -2x + 8 - 8 = -2x
Cevap: B'dir.
Soru22: |x-4| + |x| = 8 denklemini sağlayan x değerle�*rinin toplamı kaçtır?
A) 2 B) 4 C) 5 D) 6 E) 10 (2001-ÖSS)
ÇÖZÜM
Mutlak değerin içini 0 yapan değerler x = 4 ve x = 0 dır. x < 0 için -x + 4-x = 8 olur.
-x + 4-x = 8 olur.
-2x = 4 => x = - 2 dir.
0 < x < 4 için -x + 4 + x = 8 olur.
-x + 4 + x = 8 olur.
4 = 8 olduğundan bu aralıkta sağlayan x değeri yoktur. x > 4 için x - 4 + x = 8 olur.
x - 4 + x = 8 olur.
2x = 12 => x = 6 dır.
x değerleri toplamı -2 + 6 = 4 olur.
Cevap: B'dir.
Soru 23: x < 0 < y olduğuna göre
3. |x-y|
|y+|x| |
y+ işleminin sonucu aşağıdakilerden hangisidir?
A)-3x B)-3y C) 3 (x + y) D) - 3 E) 3 (1995-ÖSS)
ÇÖZÜM
3 |x - y| ifadesinde (x - y) < 0 olduğundan
3 |x - y| = - 3 (x - y) olur.
Benzer şekilde x<0 => |x| = - x olur.
| y + |x| | = |y-x| = y-x
+
3(x-y) = -3(x-y) =3
y-x -(x-y)
Cevap: E'dir...
 mutlak değer (ya da mutlak değer fonksiyonu bir gerçel sayının işaretsiz sayısal değerini verir. Örneğin
mutlak değer (ya da mutlak değer fonksiyonu bir gerçel sayının işaretsiz sayısal değerini verir. Örneğin 3; hem 3'ün hem de −3'ün mutlak değeridir. Bilgisayarlarda ise
3; hem 3'ün hem de −3'ün mutlak değeridir. Bilgisayarlarda ise bu fonksiyonu ifade etmek için kullanılan matematiksel fonksiyon genelde abs(...)'dir (Örneğin: abs(−8)=|−8|=8 gibi).
bu fonksiyonu ifade etmek için kullanılan matematiksel fonksiyon genelde abs(...)'dir (Örneğin: abs(−8)=|−8|=8 gibi).Mutlak değer fonksiyonunun gerçel sayılarla kullanımı dışında
 geniş bir matematiksel kullanım alanı vardır. Örneğin
geniş bir matematiksel kullanım alanı vardır. Örneğin mutlak değer karmaşık sayılar gibi kümeler için de tanımlanabilir.
mutlak değer karmaşık sayılar gibi kümeler için de tanımlanabilir. Mutlak değer fonksiyonunun gerçel sayılardaki grafiği.
Mutlak değer fonksiyonunun gerçel sayılardaki grafiği.[değiştir]
Gerçel sayılar
Her a
 gerçel sayısının mutlak değeri | a |
gerçel sayısının mutlak değeri | a |  şeklinde ifade edilir ve şu şekilde tanımlanır:
şeklinde ifade edilir ve şu şekilde tanımlanır: Yukarıda da görüldüğü gibi a'nın mutlak değeri ya artı ya da sıfır değerini alacak
Yukarıda da görüldüğü gibi a'nın mutlak değeri ya artı ya da sıfır değerini alacak hiç bir zaman eksi değeri almayacaktır.
hiç bir zaman eksi değeri almayacaktır.Geometrik anlamda
 bir gerçel sayının mutlak değeri onun sayı doğrusunda sıfıra olan uzaklığıdır. Daha genel anlamdaysa mutlak değer iki reel sayı arasındaki farkı
bir gerçel sayının mutlak değeri onun sayı doğrusunda sıfıra olan uzaklığıdır. Daha genel anlamdaysa mutlak değer iki reel sayı arasındaki farkı sayı doğrusunda aralarındaki uzaklık olarak verir.
sayı doğrusunda aralarındaki uzaklık olarak verir.Aşağıdaki yordamlar bir mutlak değerin çözümünde yardımcı olabilecek önermeler içerir.
1. ÖNERME:
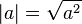
2. ÖNERME:
Mutlak değer aşağıdaki dört temel özelliğe sahiptir:
 Negatif olmama
Negatif olmama 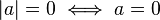 Sıfır eşitliği
Sıfır eşitliği  Çarpanlara ayrılabilme
Çarpanlara ayrılabilme  Alt toplananlara ayrılabilme
Alt toplananlara ayrılabilme3. ÖNERME:
Mutlak değerin diğer önemli özellikleri ise:
 Simetri
Simetri 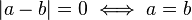 a ve b eştir
a ve b eştir 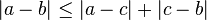 Üçgen eşitsizliği
Üçgen eşitsizliği  Bölmenin ayrılması (çarpanlara ayrılabilirlik gibi)
Bölmenin ayrılması (çarpanlara ayrılabilirlik gibi)  (Alt toplananlara ayrılabilirlik)
(Alt toplananlara ayrılabilirlik)Diğer iki kullanışlı eşitsizlikler ise:

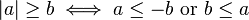
Aşağıdakilerse genelde eşitsizlik çözümünde kullanılır; örneğin:


 [değiştir]
[değiştir]Karmaşık sayılar

Karmaşık sayılara kadar olan kısımda
 verilen mutlak değer özellikleri karmaşık sayılar kümesine aynen uygulanamaz. Önerme 1'i ele alırsak:
verilen mutlak değer özellikleri karmaşık sayılar kümesine aynen uygulanamaz. Önerme 1'i ele alırsak: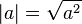 her gerçel sayının bir karmaşık sayı olduğunu ve
her gerçel sayının bir karmaşık sayı olduğunu ve
bir karmaşık sayının
 olduğunu düşünürsek göreceğiz ki
olduğunu düşünürsek göreceğiz ki gerçel sayılarda y katsayısı 0'a eşit. Öyleyse gerçekte z'nin mutlak değer (ya da karmaşık sayılarda bazen modül olarak adlandırılır) şu şekilde tanımlanabilir.
gerçel sayılarda y katsayısı 0'a eşit. Öyleyse gerçekte z'nin mutlak değer (ya da karmaşık sayılarda bazen modül olarak adlandırılır) şu şekilde tanımlanabilir. Öyleyse bir gerçel sayıda bu işlemi şöyle gerçekleştirebiliriz:
Öyleyse bir gerçel sayıda bu işlemi şöyle gerçekleştirebiliriz: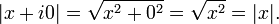 Mutlak değer bir sayının orijine uzaklığını verir. Karmaşık sayılar iki boyutlu düzlem üzerinde incelendiğinden Pisagor teoremi iki nokta arasındaki uzaklığı bulmada işimize yarayacaktır.Karmaşık düzlemde iki karmaşık sayı arasındaki uzunluğu bulmak içinse aynı gerçel sayılardaki gibi iki sayının farkının mutlak değerini alırız.
Mutlak değer bir sayının orijine uzaklığını verir. Karmaşık sayılar iki boyutlu düzlem üzerinde incelendiğinden Pisagor teoremi iki nokta arasındaki uzaklığı bulmada işimize yarayacaktır.Karmaşık düzlemde iki karmaşık sayı arasındaki uzunluğu bulmak içinse aynı gerçel sayılardaki gibi iki sayının farkının mutlak değerini alırız.Karmaşık sayılar yukarıda verilen 2. ve 3. önermelerin tüm özelliklerini taşır. Bununla beraber

 ise
ise ve
ve z karmaşık sayısının eşlenik'i ise
z karmaşık sayısının eşlenik'i ise açıkça görülür ki:
açıkça görülür ki:
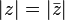
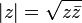
doğru üzerinde x sayısının sıfıra olan uzaklığına x in mutlak değeri denir ve │x│ ile gösterilir.
x
 R nin elemanıdır ve
R nin elemanıdır ve│x│ ={x
 x > 0 ise
x > 0 ise{-x
 x < 0 ise
x < 0 iseşeklinde tanımlanır.
│f(x)│ ={f(x)
 f(x) > 0 ise
f(x) > 0 ise{-f(x)
 f(x)< 0 ise
f(x)< 0 iseÖrnek: x =-3 için │x-5│ - │x+2│ ifadesinin eşiti kaçtır?
Çözüm: │-3-5│ - │-3+2 │ = 8-1=7
Örnek: a<b<0olduğuna göre

│a+b│ - │a-b │ ifadesinin eşiti nedir?
Çözüm: │a+b│ - │a-b│ = -(a+b) -[ -(a-b) ]
=-a-b+a-b
=-2b
ÖZELLİKLERİ
a
 b elemandır R için
b elemandır R için1) │a│≥ 0 dır
2) │a │ = │ -a│
3) - │ a│≤a ≤│a│
4) │a.b│ = │a│.│b │
5) b�* 0 için │a/b │= │a│ / │b │
6) │IaI-IbI│≤│a+b│ < │a│ + │b │ (üçgen eşitsizliği)
7) n elemanıdır Z+ olmak üzere │an │ = │a│n
8) a> 0
 x elemanıdır R ve │x│< a ise -a <x <a
x elemanıdır R ve │x│< a ise -a <x <a9) a>0
 x elemanıdır R
x elemanıdır R │x│≥ a ise x≥ a veya x ≤ -a dır.
│x│≥ a ise x≥ a veya x ≤ -a dır.10)I-aI=IaI
 Ia-bI=Ib-aI
Ia-bI=Ib-aI11)I f(x) I = a ise f(x )= a veya f(x) = -a
12)I f(x) I < a ise -a< f(x) < a
13)I f(x) I > a ise f(x) > a U -f(x) > a
İSPATLAR
Öz.1)a = 0 ise IaI = I0I = 0
a > 0 ise IaI = a >0
a < 0 ise IaI = -a >0 dır.
O halde IaI > 0 dır.
Öz.2)a ve -a sayılarının 0 dan uzaklıkları eşit olduğundan IaI=I-aI dır.
Öz.6) a elemanıdır R için -IaI ≤ a ≤ IaI
b elemanıdır R için -IbI ≤ b≤ IbI
+
-IaI-IbI≤a+b≤IaI+IbI
O halde Ia+bI < IaI+IbI dir.
Öz.7) a
 b elemanıdır R için Ia.bI=IaI.IbI idi.
b elemanıdır R için Ia.bI=IaI.IbI idi.Ia nI=Ia.a.a...aI=IaI.IaI.IaI...IaI=IaIn dir.
(n tane) ( n tane )
Öz.3)a sayısı için a<0
 a=0
a=0 a>0 durumlarından biri vardır.
a>0 durumlarından biri vardır.a)a < 0 ise IaI = -a dır.
IaI > 0 olduğundan -IaI < 0 dır.
-IaI= a <0 < IaI ise -IaI < a < IaI dır.
b)a=0 ise IaI = I0I = 0 ve -Ia I= 0 olacağından –IaI < a < IaI dır.
c)a > 0 ise IaI = a ve -IaI < 0 dır.
-IaI≤ 0≤ IaI = a ise -IaI < a < IaI dır.
MUTLAK DEĞERLİ DENKLEMLER
Soru: I3x-7I = 5 denklemini çözünüz.
Çözüm:I3x-7I = 5 ise; 3x-7 = 5 veya 3x-7 = -5 olur.
1- 3x-7 = 5 2- 3x-7=-5
3x = 12 3x = 2
x = 4 x = 2/3
Ç={4
 2/3}
2/3}Soru:Ix-7I = 7-x eşitliğini sağlayan kaç tane doğal sayı vardır?
Çözüm: Ix-7I = 7-x ise
x-7 < 0 ise x < 7olup x doğal sayıları 0
 1
1 2
2 3
3 4
4 5
5 6
6 7 dir.
7 dir.O halde 8 tane doğal sayı vardır.
Soru: = 2 denkleminin çözüm kümesi nedir ?
Çözüm: = 2
5-2x/3=2 veya 5-2x/3= -2
5-2x = 6 veya 5-2x = -6
x = -1/2 veya x = 11/2
Ç ={-1/2
 11/2}
11/2}Soru:I 4+I2x-3I I = 5 denklemini sağlayan x reel sayılarının toplamı nedir?
Çözüm: I 4+I2x-3I I = 5
4+I2x-3I = 5 veya 4+I2x-3I = -5
I2x-3I = 1 veya I2x-3I = -9
2x-3 = 1 veya 2x-3 = -1 Çözüm:O
x = 2 x = 1
O halde x+x = 2+1 = 3 olur.
Uyarı:Hiçbir reel sayının mutlak değeri negatif olamayacağından
 denklemin çözüm kümesi boş küme () olur.
denklemin çözüm kümesi boş küme () olur.MUTLAK DEĞERLİ EŞİTSİZLİKLER
Soru: Ix-7I < 3 eşitsizliğinin çözüm kümesini bulunuz.
Çözüm: Ix-7I < 3 = -3 < x-7 < 3 = -3+7 < x < 3+7
=4<x<10 Ç={5
 6
6 7
7 8
8 9}
9}Soru:I 3x+2 I+9 > 2 eşitsizliğini çözünüz.
Çözüm:I 3x+2I+9 > 2 = I 3x+2I > -7
***Bu eşitsizlik x in her değeri için sağlanır.Bu nedenle; Çözüm kümesi R dir.
Soru: I Ix-5I-2 I < 3 eşitsizliğini sağlayan kaç tane tamsayı vardır?
Çözüm:I Ix-5I-2 I < 3 = -3 < Ix-5I -2 < 3
= -1 < Ix-5I < 5
Ix-5I >-1 eşitsizliği daima doğrudur.
Ix-5I < 5 = -5 < x-5 < 5
= 0 < x < 10
Bu aradaki tamsayılar 1
 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9 olup 9 tamsayı vardır.
9 olup 9 tamsayı vardır.Soru: I 2x-7 I < 2 eşitsizliğini sağlayan kaç tane tamsayı vardır?
Çözüm:I 2x-7 I < 2 = -2 < 2x-7 < 2
= -2+7 < 2x < 2+7
= 5 < 2x < 9
= 5/2 < x < 9/2
Bu durumda çözüm kümesi {3
 4} olur.
4} olur.Soru: I 3x+1 I > -8 denkleminin çözüm kümesini bulunuz.
Çözüm: x elemanıdır R için I 3x+1 I > 0 olduğundan
I 3x+1 I > -8 eşitsizliği daima doğrudur. Buna göre denklemin çözüm kümesi Reel sayılar kümesidir.
Soru: I 3-3x I < 9 eşitsizliğinin R deki çözüm kümesi nedir?
a) 0<x<2 b) -2<x<4 c) -1<x<0 d) 0<x<2 e) 2<x<4
Çözüm: I 3-3x I<9 = -9 < 3-3x < 9
= -9+3 < 3x < 9+3
= -6 < 3x < 12
= -6/3 < x < 12/3
= -2 < x < 4 ( Cevap B dir.)
Soru: 1 < Ix-2I < 3 eşitsizliğini sağlayan kaç tane tamsayı vardır?
Çözüm: 1 < Ix-2I < 3 = 1 < x-2 < 3
= 1+2 < x < 3+2
= 3 < x < 5
Eşitsizliği oluşturan tamsayılar = {3
 4
4 5} tir.
5} tir.MUTLAK DEĞER İLE İLGİLİ KARIŞIK
ALIŞTIRMALAR
Soru 3: |x| 2 => -2<x<2 dir.
Soru 4: |x| 2 => x > 2 veya x < -2 dir.
Soru 5: |x-1| = 3 => x-1=3 veya x - 1 = -3
x = 4 veya x = -2 dir.
Soru 6: a<b<0<c olmak üzere;
a +c + b-c+c - a
= -a + c - (b - c) + c – a
= -a + c-b + c + c- a
= 3c - 2a - b dir.
Soru 7:x-5= 3 => x - 5 = 3 veya x -5 = -3 tür.
x = 8 veya x = 2
x = 8 veya x =- 8 veya
x = 2 veya x =- 2 dir.
Ç.K. = {-8
 -2
-2 2
2 8} dir.
8} dir.Soru 8: ||x-l| + 4| = 6=>x-1 + 4 = 6 veya
x-1 + 4 = -6 lx-1l = 2 veya lx-1l = -10 olur.
x-1 = - 10 olamayacağından kök yoktur.
x-1 = 2 ise x - 1 = 2 veya x - 1 = -2 x = 3 veya x = -1 dir.
Ç.K = {-1
 3}
3}Soru 9: I 3x-1 I+5 = 0 denkleminin çözüm kümesi nedir?
Çözüm: I 3x-1 I+5 = 0 ise I 3x-1 I = -5 olur.
*** a elemanıdır R için IaI > 0 dır.
Bu nedenle sorunun çözüm kümesi O dir.
Soru 10: I Ix-4I -5 I = 10 denklemini sağlayan x değerlerini bulunuz.
Çözüm: I Ix-4I –5 I = 10
Ix-4I-5 =10 veya Ix-4I-5 = -10
Ix-4I = 5 veya Ix-4I = -5
Ç = {O}
x-4 = 15 veya x-4 = -15 x = 19 veya x = -14
Soru11: I Ix-1I+5 I = 8 denkleminin kökleri toplamı kaçtır?
a) -2 b) 0 c) 2 d) 4 e)14
Çözüm: I Ix-1I+5 I = 8
I Ix-1I+5 I = 8 veya I Ix-1I+5 = -8
Ix-1I = 3 veya Ix-1I = -13
Ç = {O}
x-1 = 3 veya x-1 = -3
x = 4 veya x = -2
x+x = 4+(-2) = 2 ( Cevap C dir.)
Soru 12: I Ix-2I-3 I = 7 denkleminin kökleri toplamı kaçtır?
a) 2 b) 4 c) 8 d) 10 e) 12
Çözüm: I Ix-2I-3 I = 7
Ix-2I-3 = 7 veya Ix-2I-3 = -7
Ix-2I = 10 veya Ix-2I = -4
Ç = {O}
x-2 = 10 veya x-2 = -10
x = 12 veya x = -8
x+x = 12-(-8) = 4 ( Cevap B dir.)
Soru 13: I 7-(3-I-5I) I işleminin sonucu nedir?
A) 4 B) 5 C) 6 D) 7 E) 9
Çözüm:
I 7-(3-I-5I) I = I 7-[3- -(-5)] I
= I 7-[3-5] I
= I 7-(-2) I
= I 7+2 I
= I 9 I = 9
Soru 14: I Ix-2I-5 I = 1 denklemini sağlayan x tam sayıları nelerdir?
a) 3
 6
6 -3
-3 -6 b) 4
-6 b) 4 8
8 -3
-3 -8 c) 7
-8 c) 7 9
9 5 d) 8
5 d) 8 -4
-4 6
6 -2 e) 2
-2 e) 2 -2
-2Çözüm: I Ix-2I-5 I
Ix-2I-5 = 1 veya Ix-2I-5 = -1
Ix-2I = 6 veya Ix-2I = 4
x-2 = 6 veya x-2 = -6 x-2 = 4 veya x-2 = -4
x = 8 x = -4 x = 6 x = -2
Soru 15: Ix+2I < 4 eşitsizliğini sağlayan kaç tane tamsayı vardır?
a) 13 b) 9 c) 8 d) 7 e) 6 (ÖSS 1999)
Çözüm:
Ix+2I < 4 = -4 < x + 2 <4
= -6 < x < 2
Eşitsizliği oluşturan tamsayılar –6
 -5
-5 -4
-4 -3
-3 -2
-2 -1
-1 0
0 1
1 2 dir. ( Cevap A dır.)
2 dir. ( Cevap A dır.)Soru 16: IxI < 6 olduğuna göre
 x-2y+2 = 0 koşulunu sağlayan kaç tane y tamsayısı vardır?
x-2y+2 = 0 koşulunu sağlayan kaç tane y tamsayısı vardır?a) 7 b) 6 c) 5 d) 4 e) 3 (ÖSS 2000)
Çözüm:
IxI 0 dan küçük olmayacağından IxI 0
 1
1 2
2 3
3 4
4 5
5 6 olabilir.
6 olabilir.x-2y+2 = 0 koşulunu çift sayılar oluşturur.Bunlar 0
 2
2 4
4 6 dır.Bu sayılar y yi tamsayı yapar. ( Cevap D dir.)
6 dır.Bu sayılar y yi tamsayı yapar. ( Cevap D dir.)Soru 17:
f(x) = 12 fonksiyonunun en büyük değeri
Ix-1I+Ix+3I
nedir?
a) 2 b) 3 c) 4 d) 5 e) 6
Çözüm:
x elemanıdır [-3
 1] için f(x) en büyük olur. X = -3 ise
1] için f(x) en büyük olur. X = -3 ise
f(-3) = 12 = 12/4 =3 tür.
I-3-1I+I-3+3I
( Cevap B dir.)
Soru 18:x-1 6 olduğuna göre
 x - 2y + 2 = O koşulunu sağlayan kaç tane y tamsayısı vardır?
x - 2y + 2 = O koşulunu sağlayan kaç tane y tamsayısı vardır?A) 7 B) 6 C) 5 D) 4 E) 3 (2000-ÖSS)
ÇÖZÜM
x-2y + 2 = 0 => x = 2y- 2 dir.
x < 6 => 2y - 2 6 => -6 2y - 2 < 6 dır.
Buradan
 -4 < 2y < 8 => -2 < y < 4 bulunur.
-4 < 2y < 8 => -2 < y < 4 bulunur.Bu koşulu sağlayan y tamsayıları -2
 -1
-1 0
0 1
1 2
2 3
3 4 olup 7 tanedir.
4 olup 7 tanedir.Cevap: A'dır.
Soru 19:x+24 eşitsizliğini sağlayan kaç tane tamsayı vardır?
A) 13 B) 9 C) 8 D) 7 E) 6 (1999-ÖSS)
ÇÖZÜM
x+24 ise < 4 ise -4 < x + 2 < 4
-4-2<x+2-2<4-2
-6 < x < 2
x = -6
 -5
-5 -4
-4 -3
-3 -2
-2 -1
-1 O
O 1
1 2 olup 9 tane tamsayı değeri vardır.
2 olup 9 tane tamsayı değeri vardır.Cevap: B'dir.
Soru 20: x < 0 olmak üzere x-|x-8| - 8 ifadesi aşağı�*dakilerden hangisine eşittir?
A)16 B)-2x C)-4x D)-2x+16 E)-4x+16 (1999-ÖSS)
ÇÖZÜM
x-|x-8| - 8 = ?
x-8| = -(x-8) = -x+8
(-)
= x-(-x+8) - 8 |2x-8|-8
(-)
= - (2x - 8) - 8 = -2x + 8 - 8 = -2x
Cevap: B'dir.
Soru22: |x-4| + |x| = 8 denklemini sağlayan x değerle�*rinin toplamı kaçtır?
A) 2 B) 4 C) 5 D) 6 E) 10 (2001-ÖSS)
ÇÖZÜM
Mutlak değerin içini 0 yapan değerler x = 4 ve x = 0 dır. x < 0 için
 -x + 4-x = 8 olur.
-x + 4-x = 8 olur.-2x = 4 => x = - 2 dir.
0 < x < 4 için
 -x + 4 + x = 8 olur.
-x + 4 + x = 8 olur.4 = 8 olduğundan bu aralıkta sağlayan x değeri yoktur. x > 4 için
 x - 4 + x = 8 olur.
x - 4 + x = 8 olur.2x = 12 => x = 6 dır.
x değerleri toplamı -2 + 6 = 4 olur.
Cevap: B'dir.
Soru 23: x < 0 < y olduğuna göre
3. |x-y|
|y+|x| |
y+ işleminin sonucu aşağıdakilerden hangisidir?
A)-3x B)-3y C) 3 (x + y) D) - 3 E) 3 (1995-ÖSS)
ÇÖZÜM
3 |x - y| ifadesinde (x - y) < 0 olduğundan
3 |x - y| = - 3 (x - y) olur.
Benzer şekilde x<0 => |x| = - x olur.
| y + |x| | = |y-x| = y-x
+
3(x-y) = -3(x-y) =3
y-x -(x-y)
Cevap: E'dir...




Hiç yorum yok:
Yorum Gönder